그래프 이론이란?
우리가 길을 찾아가거나, 인터넷에서 친구들과 소통하거나, 최적의 배달 경로를 찾을 때, 눈에 보이지 않는 강력한 수학적 원리가 작동하고 있습니다. 바로 그래프 이론(Graph Theory)입니다.
그래프 이론은 점(노드)과 선(엣지)으로 이루어진 구조를 연구하는 수학 분야로, 오늘날 네트워크 설계, 교통 시스템, 데이터 분석 등 다양한 분야에서 활용됩니다.
쾨니히스베르크의 다리 문제: 그래프 이론의 시작
18세기 프로이센(현재 러시아의 칼리닌그라드)에는 한 도시를 가로지르는 강과 7개의 다리가 있었습니다. 당시 사람들은 이런 질문을 던졌습니다.
"모든 다리를 한 번씩만 지나서 다시 출발점으로 돌아오는 것이 가능할까?"
이 단순한 질문이 세계 최초의 그래프 문제로 남게 될 줄은 아무도 몰랐습니다. 하지만, 이를 수학적으로 탐구한 사람이 있었습니다. 바로 레온하르트 오일러(Leonhard Euler, 1707–1783)입니다.
오일러는 이 문제를 연구하면서 도시의 지형을 단순화했습니다. 섬과 강변을 점(노드)으로, 다리를 선(엣지)으로 표현한 것이죠. 그 결과, 오일러는 다음과 같은 중요한 사실을 발견했습니다.
어떤 그래프에서 한붓그리기(오일러 회로)가 가능하려면, 모든 점의 연결선(엣지)의 개수가 짝수여야 한다.
즉, 7개의 다리를 한 번씩만 지나면서 원래 자리로 돌아오는 것은 불가능하다는 것을 증명한 것입니다. 이렇게 탄생한 개념이 바로 그래프 이론의 시초가 되었습니다.

그래프 이론의 발전: 해밀턴 경로와 최단 경로 문제
오일러 이후 그래프 이론은 더욱 발전했습니다. 특히, 해밀턴 경로와 다익스트라 알고리즘은 그래프 이론에서 중요한 개념으로 자리 잡았습니다.
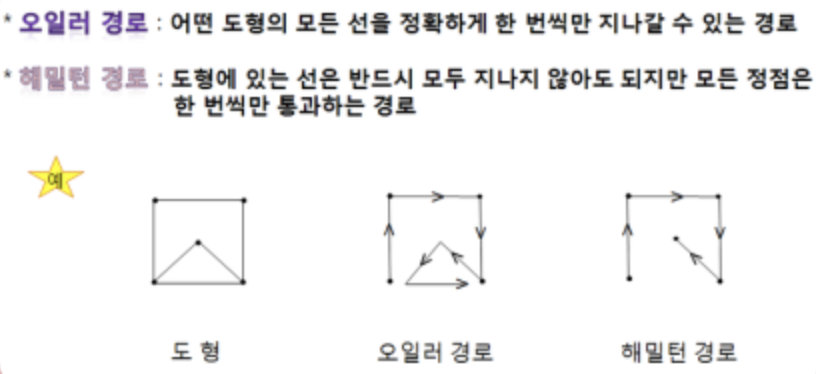
🔹 해밀턴 경로 (Hamiltonian Path)
해밀턴 경로는 모든 노드를 정확히 한 번씩 지나가는 경로를 의미합니다.
오일러 경로(Eulerian Path)와의 차이점은 무엇일까요?
- 오일러 경로는 모든 엣지를 한 번씩 지나가는 경로
- 해밀턴 경로는 모든 노드를 한 번씩 방문하는 경로
이 개념은 19세기 수학자 **윌리엄 로완 해밀턴(W. R. Hamilton)**이 연구하면서 널리 알려졌습니다. 해밀턴 경로가 존재하는지 여부를 찾는 문제는 NP-완전(NP-complete) 문제로, 매우 어려운 수학적 문제로 알려져 있습니다.
실생활 활용 예시
- 배달 차량이 모든 도시를 한 번씩 방문하는 최적의 경로 찾기
- 여행자가 모든 관광지를 한 번씩 들르는 여행 계획 세우기
🔹 다익스트라 알고리즘 (Dijkstra’s Algorithm)
해밀턴 경로가 그래프에서 특정 패턴을 찾는 문제라면, 다익스트라 알고리즘(Dijkstra’s Algorithm)은 가장 짧은 경로를 찾는 알고리즘입니다.
이 알고리즘은 1956년 네덜란드의 컴퓨터 과학자 에츠허르 다익스트라(Edsger W. Dijkstra)가 개발한 방법으로, 그래프에서 한 지점에서 다른 지점까지의 최단 거리를 찾는 데 사용됩니다.
실생활 활용 예시
- 네비게이션 앱이 최단 경로를 찾는 원리
- 인터넷 네트워크에서 데이터 패킷의 최적 이동 경로 찾기
- 지하철에서 최소 환승으로 목적지에 도착하는 경로 계산
오일러의 위대한 업적들
오일러는 그래프 이론뿐만 아니라 수학의 거의 모든 분야에 기여했습니다.
1. 오일러의 공식 (Euler’s Formula)
그는 수학에서 가장 아름다운 방정식 중 하나를 발견했습니다.
eiπ+1=0e^{i\pi} + 1 = 0
이 공식은 수학에서 가장 중요한 다섯 개의 수(𝑒, 𝑖, 𝜋, 1, 0)를 하나의 방정식으로 연결하며, 과학과 공학에서도 광범위하게 사용됩니다.
2. 오일러의 다면체 정리 (Euler's Polyhedron Formula)
V−E+F=2V - E + F = 2
(여기서 V는 꼭짓점(Vertex), E는 모서리(Edge), F는 면(Face)입니다.)
이 공식은 기하학에서 입체 도형의 구조를 설명하는 핵심 원리 중 하나로, 건축과 컴퓨터 그래픽 등에서 활용됩니다.
3. 유체 역학의 오일러 방정식
오일러는 물리학에도 깊은 영향을 미쳤습니다. 그의 오일러 방정식은 유체(액체나 기체)의 움직임을 설명하는 기본 방정식으로, 항공기 설계나 기상 예측 등에 사용됩니다.
그래프 이론이 현대 사회에 미친 영향
오일러가 시작한 그래프 이론은 오늘날 우리가 사는 세상을 설명하는 중요한 도구가 되었습니다.
- 네트워크 분석: 인터넷, 소셜 미디어, 전력망, 교통망 등 모든 연결 구조 분석
- 컴퓨터 과학: 알고리즘, 데이터 구조, 검색 엔진 최적화
- 생물학: 유전자 네트워크, 질병 확산 모델링
- 물류 및 최적화: 최단 경로 문제, 배달 경로 최적화
- 물리학과 화학: 분자 구조 분석, 전자 이동 모델링
우리가 오늘날 인터넷을 자유롭게 탐색하고, GPS를 사용해 최적의 길을 찾고, SNS에서 친구들과 연결될 수 있는 것도 모두 그래프 이론의 발전 덕분입니다.
'궁금증 해결 > 이과적궁금증' 카테고리의 다른 글
| 피타고라스 정리란? 피타고라스 정리의 개요, 기원, 응용분야, 피타고라스의 업적 (2) | 2025.01.30 |
|---|---|
| 베이즈 정리(Bayes' Theorem): 불확실성을 다루는 강력한 도구 (2) | 2025.01.29 |
| 오일러의 다면체 정리: 다면체 속 숨겨진 아름다움 (0) | 2025.01.19 |
| 맥스웰 방정식이란? 맥스웰 방정식의 내용, 의의, 활용 (3) | 2025.01.12 |
| 라그랑주 승수법이란? 라그랑주 승수법의 이론, 예시, 역사, 활용분야 (114) | 2023.07.09 |



