피타고라스 정리란?
피타고라스의 정리(Pythagorean Theorem)는 직각삼각형에서 세 변 사이의 관계를 설명하는 고전적인 정리입니다. 다음과 같은 수식으로 표현됩니다:
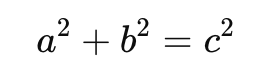
여기서:
- a, : 직각을 이루는 두 변의 길이
- c : 빗변(직각을 낀 변이 아닌 가장 긴 변)의 길이
이 정리는 단순한 기하학적 관계를 넘어 수학, 물리학, 공학, 그리고 컴퓨터 과학의 다양한 분야에서 중요한 역할을 합니다.
이론의 기원
피타고라스의 정리는 기원전 6세기경 고대 그리스의 철학자이자 수학자인 피타고라스(Pythagoras, 기원전 570~495년)에 의해 널리 알려졌습니다. 하지만 이 정리는 사실 그보다 훨씬 오래전부터 존재했습니다.
- 기원전 1900년경 바빌로니아 수학자들이 이 정리를 사용한 증거가 발견되었습니다.
- 고대 중국(주나라)에서도 "구장산술(九章算术)"에서 유사한 관계를 설명한 기록이 남아 있습니다.
- 인도에서는 바우다야나(Baudhayana)라는 학자가 기원전 8세기경 비슷한 수식을 기록하였습니다.
즉, 피타고라스의 정리는 피타고라스가 최초로 발견한 것이 아니라, 그가 이를 체계적으로 연구하고 증명하며 수학적 체계를 확립한 데서 그의 이름이 붙게 된 것입니다.

피타고라스와 그의 업적
피타고라스는 단순히 피타고라스의 정리를 발견한 것뿐만 아니라, 수학과 철학의 다양한 분야에서 중요한 업적을 남겼습니다.
- 피타고라스 학파: 그는 "모든 것은 수로 이루어져 있다"는 철학을 주장하며 수학과 자연을 연결하려 했습니다.
- 정수의 신비: 완전수(perfect number), 친화수(amicable number) 등 수 이론의 기초 개념을 연구했습니다.
- 음계와 수학: 음악에서 옥타브와 수학적 비율을 연구하며 현대 음악 이론의 기초를 마련했습니다.
- 황금비(Golden Ratio): 아름다움과 조화를 설명하는 수학적 개념을 연구하는 데 영향을 주었습니다.
피타고라스 정리의 의의
피타고라스의 정리는 직각삼각형에 대한 단순한 정리처럼 보일 수 있지만, 수학적 사고의 본질을 보여주는 대표적인 사례입니다. 이 정리는 공간과 거리의 개념을 정량적으로 설명하는 최초의 체계적인 도구로 활용되었으며, 이후 수학의 발전에 큰 영향을 미쳤습니다.
특히, 피타고라스의 정리는 유클리드 기하학의 근본 원리 중 하나가 되었으며, 현대 과학과 공학에서도 필수적인 도구로 사용됩니다.
피타고라스 정리의 응용 분야
1. 삼각측량과 GPS
오늘날 GPS 시스템은 위성에서 지구 표면까지의 거리를 계산할 때 피타고라스의 정리를 활용합니다. 삼각측량(triangulation) 기법을 통해 위치를 정확히 파악하는 데 필수적인 개념입니다.
2. 건축 및 공학
건물과 다리의 구조적 안정성을 분석할 때 피타고라스 정리를 사용하여 각도와 길이를 계산합니다.
3. 컴퓨터 그래픽스와 게임 개발
컴퓨터에서 2D 또는 3D 공간 내에서 객체 간의 거리를 계산할 때 피타고라스의 정리가 활용됩니다.
4. 물리학과 역학
운동하는 물체의 속도와 가속도를 분석할 때, 직각삼각형을 이용하여 힘의 합성과 분해를 수행합니다.
5. 전자기학과 회로 이론
교류 전기 회로에서 저항, 인덕턴스, 커패시턴스를 삼각법으로 계산할 때 피타고라스 정리가 등장합니다.
결론
피타고라스의 정리는 단순한 삼각형 공식이 아니라, 세상을 수학적으로 이해하는 데 필수적인 도구입니다. 기원전부터 사용되어 온 이 정리는 오늘날에도 다양한 분야에서 활용되며, 과학과 기술의 발전에 기여하고 있습니다.
우리가 매일 접하는 기술과 과학 속에도 이러한 수학적 원리가 숨겨져 있습니다.
'궁금증 해결 > 이과적궁금증' 카테고리의 다른 글
| 정보이론(Information Theory)이란? 데이터와 통신의 근본 원리 정보이론의 개요, 기원, 활용분야 (0) | 2025.01.31 |
|---|---|
| 베이즈 정리(Bayes' Theorem): 불확실성을 다루는 강력한 도구 (2) | 2025.01.29 |
| 오일러와 그래프 이론: 7개의 다리에서 시작된 네트워크의 혁명 (1) | 2025.01.22 |
| 오일러의 다면체 정리: 다면체 속 숨겨진 아름다움 (0) | 2025.01.19 |
| 맥스웰 방정식이란? 맥스웰 방정식의 내용, 의의, 활용 (3) | 2025.01.12 |



