라그랑주 승수법이란?
라그랑주 승수법(Lagrange multiplier method)은 미분적분학에서 제한 조건이 있는 최적화 문제를 해결하는 방법 중 하나입니다. 이 방법은 제한 조건이 있는 최적화 문제를 라그랑주 항등식을 활용하여 변형하여 푸는 것을 기반으로 합니다.
라그랑주 승수법은 목적 함수와 제한 조건이 선형이거나 볼록 함수인 경우에 특히 효과적으로 사용됩니다. 이 방법을 사용하여 최적화 문제를 푸는 것은 원래의 문제를 더 쉽게 다룰 수 있게 해줍니다. 또한, 라그랑주 승수법은 제한 조건의 개수에 관계없이 적용할 수 있어서 유연하게 사용될 수 있습니다.
라그랑주 승수법의 역사
라그랑주 승수법은 18세기 프랑스의 수학자 조셉 라그랑주(Joseph-Louis Lagrange)에 의해 개발되었습니다. 라그랑주는 수학, 천문학, 물리학 등 다양한 분야에서 활약한 유명한 수학자이며, 현대적인 해석학의 기초를 마련한 한 사람으로 알려져 있습니다.
라그랑주는 1755년에 발표된 "변분법에 대한 기초"라는 논문에서 최소 작용 원리(minimum action principle)에 대해 탐구하면서 라그랑주 승수법의 개념을 처음 도입했습니다. 이 논문은 물리학 분야에서도 큰 영향을 미쳤으며, 라그랑주는 이후에도 다양한 분야에서 수학적 연구와 응용에 참여하였습니다.
라그랑주 승수법은 그 후로 계속해서 발전해왔고, 최적화 문제와 제한 조건을 동시에 고려하는 방법으로 널리 사용되었습니다. 라그랑주 승수법은 19세기 이후 경제학에서 활발하게 사용되기 시작했으며, 이후 다양한 분야에서 응용되어 왔습니다.
조셉 라그랑주의 이름을 딴 라그랑주 승수법은 수학과 과학 분야에서 가장 중요하고 효과적인 최적화 기법 중 하나로 인정받고 있습니다. 그의 기여는 수학과 물리학에서 현대적인 해석학의 발전에 큰 영향을 미쳤으며, 그의 업적은 오늘날에도 널리 알려져 있고 귀중히 여겨지고 있습니다.
라그랑주 승수법의 단계
- 주어진 최적화 문제를 정의합니다. 최적화하려는 목적 함수와 제한 조건을 명확하게 정의합니다.
- 라그랑주 함수(Lagrange function)를 설정합니다. 라그랑주 함수는 목적 함수와 제한 조건을 결합한 함수로, 다음과 같이 정의됩니다:
- L(x, λ) = f(x) - λg(x)
여기서 f(x)는 목적 함수, g(x)는 제한 조건을 나타내는 함수, λ는 라그랑주 승수(Lagrange multiplier)입니다. - 라그랑주 함수를 편미분합니다. 라그랑주 함수를 목적 변수 x와 라그랑주 승수 λ에 대해 편미분하여 각각의 편미분식을 구합니다.
- 편미분식을 활용하여 극값을 찾습니다. 편미분식을 활용하여 f(x)와 g(x)의 미분값이 0인 지점을 찾습니다. 이렇게 구한 x 값들을 기반으로 목적 함수의 극값을 계산합니다.
- 구한 x 값들이 목적 함수와 제한 조건을 모두 만족하는 최적해인지를 확인하기 위해, 제한 조건을 검증합니다. 예를 들어, 등식 제한 조건이 있는 경우 등식을 만족하는지 확인하거나, 부등식 제한 조건이 있는 경우 부등식을 만족하는지 확인합니다.
라그랑주 승수법 활용 예시
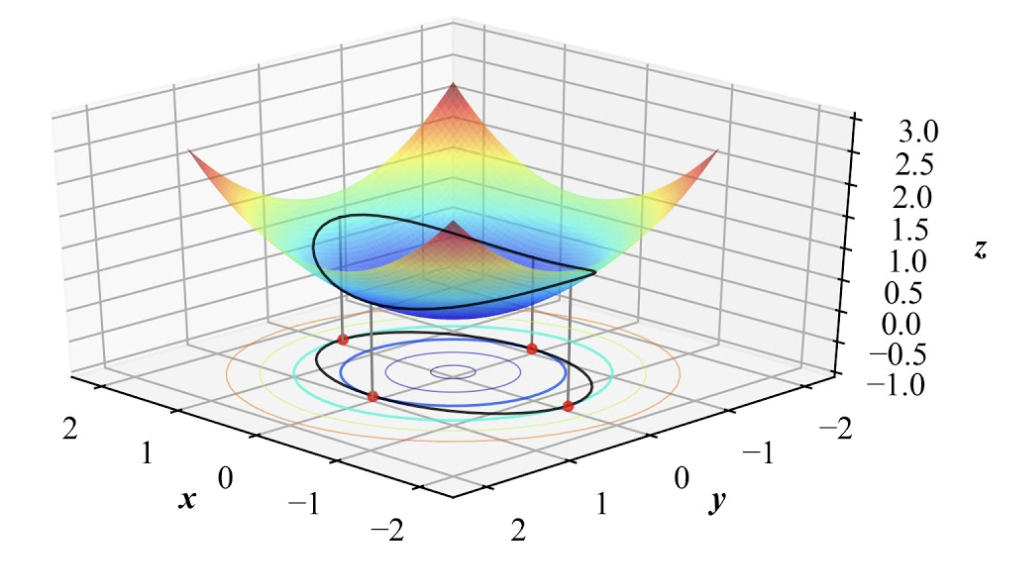
문제 : x와 y의 값이 주어졌을 때, 함수 f(x, y) = x^2 + y^2의 최소값을 구하되, 제한 조건으로 g(x, y) = x + y - 1 = 0을 만족해야 함
- 라그랑주 함수 L(x, y, λ)를 설정합니다:
- L(x, y, λ) = f(x, y) + λg(x, y) = x^2 + y^2 + λ(x + y - 1)
- L(x, y, λ)를 x, y, λ에 대해 편미분합니다:
- ∂L/∂x = 2x + λ = 0
- ∂L/∂y = 2y + λ = 0
- ∂L/∂λ = x + y - 1 = 0
- 위 세 개의 방정식을 풀어 해를 구합니다. 첫 번째와 두 번째 방정식으로부터 x = -λ/2, y = -λ/2를 얻을 수 있고, 세 번째 방정식으로부터 x + y = 1이므로 λ = -2가 됩니다.
- λ = -2를 다시 첫 번째와 두 번째 방정식에 대입하여 x = 1, y = 1을 얻습니다.
따라서, 주어진 제한 조건 하에서 함수 f(x, y) = x^2 + y^2의 최소값은 x = 1, y = 1일 때의 값인 2가 됩니다. 라그랑주 승수법을 사용하여 최소값을 구할 수 있습니다.
이 예시에서는 제한 조건으로 선형 방정식을 사용했지만, 라그랑주 승수법은 다양한 형태의 제한 조건을 다룰 수 있습니다. 라그랑주 승수법을 통해 제한 조건이 있는 최적화 문제를 해결함으로써, 목적 함수의 극값을 찾을 수 있습니다.
라그랑주 승수법의 활용분야
라그랑주 승수법은 다양한 분야에서 응용될 수 있습니다.
- 경제학: 소비자의 최적 선택 문제나 생산자의 이윤 최대화 문제에서 라그랑주 승수법을 활용하여 제한 조건을 고려한 최적해를 구합니다.
- 물리학: 그랑주 함수를 통해 운동의 최소 작용 원리나 최소 포텐셜 에너지 원리를 구할 수 있습니다. 이를 통해 운동방정식이나 여러 물리적 시스템의 동작을 설명할 수 있습니다.
- 공학: 제한된 자원을 최대로 활용하는 문제나 구조 설계에서의 최적 해석, 전기 회로 설계 등에서 라그랑주 승수법을 사용할 수 있습니다.
- 운송 문제: 최소 비용으로 물류 네트워크를 구성하는 문제에서 라그랑주 승수법을 사용하여 제한 조건을 고려한 최적 경로를 결정합니다.
- 제어 이론: 제한 조건이 있는 시스템의 최적 제어 문제에서 라그랑주 승수법을 사용하여 최적 제어 신호를 결정하거나, 시스템의 상태를 최적화하는 문제에서 라그랑주 승수법을 활용합니다.
'궁금증 해결 > 이과적궁금증' 카테고리의 다른 글
| 오일러의 다면체 정리: 다면체 속 숨겨진 아름다움 (0) | 2025.01.19 |
|---|---|
| 맥스웰 방정식이란? 맥스웰 방정식의 내용, 의의, 활용 (3) | 2025.01.12 |
| 미분방정식이란? 미분방정식의 역사, 미분방정식의 종류, 미분방정식의 활용분야 (1) | 2023.06.19 |
| 편미분이란? 편미분의 역사, 편미분 관련 주요 정의, 편미분의 활용분야 (0) | 2023.06.18 |
| 테일러 급수란? 테일러급수의 용도, 증명, 역사 (1) | 2023.06.06 |



